Что такое “малые группы”?
Соционические типы можно объединять в группы, обладающие общими свойствами – разумеется, объединять не произвольно, а опираясь на определённые закономерности. Чаще всего в соционике используются группы по 4 типа, которые называются “малыми группами” (термин предложил Г.Р.Рейнин) или “кватернионами” (термин, предложенный В.В.Гуленко, среди социоников не прижился).
Всего в соционике известно 35 «малых групп», образованных из социотипов, у которых совпадает три (два ортогональных и третий связанный с ними) из 15 «признаков Рейнина».
Каждая из этих групп состоит из 4 информационных аспектов, таким образом, потенциально имеется для рассмотрения 35×4=140 этих аспектов.
Чем интересны и полезны малые группы
Вот лишь некоторые примеры:
1. Психодиагностика. Характеристика малой группы (например, “клуба” интуитов-логиков) – это гораздо больше, чем просто сумма характеристик входящих в группу типов. Более того, целый ряд личностных свойств просто невозможно втиснуть в прокрустово ложе признаков из “базиса Юнга”. Например, такое свойство, как общительность, невозможно привязать только к экстраверсии или только к этике.
2. Работа с кадрами. Знание особенностей общения внутри той или иной группы помогает как грамотно сочетать людей в рабочем или учебном коллективе, так и создавать специфические группы для разных целей: для “мозгового штурма”, для долговременного сотрудничества и т.д.
3. Обучение. Такие группы, как “клубы” (установки на род деятельности) в значительной мере определяют способность ученика к восприятию и усвоению той или иной информации, а также способность преподавателя адекватно передать ту или иную информацию, его “стиль обучения”. Эти знания оказываются полезны при работе со школьными и вузовскими коллективами, при создании индивидуальных преподавательских методик.
4. Психотерапия. Как утверждают Г.Рейнин и С.Гиндин, в ходе исследований им удалось обнаружить, что взаимодействие в некоторых группах (в частности, “соционические темпераменты”, они же “букеты”) ухудшает не только психологическое, но и физическое состояние участников, в то время как взаимодействие в других группах (т.наз. “группах здоровья”) – напротив, улучшает. Жаль, что подробных исследований в этом направлении не проводилось.
Малые группы до соционики
Карл Густав Юнг
Впервые малые группы появляются в работе самого Карла Густава Юнга “Психологические типы”. Всего их четыре: рациональные интровертированные, рациональные экстравертированные, иррациональные интровертированные и иррациональные экстравертированные типы. Юнг достаточно подробно описывает свойства всех четырёх групп.
Типоведение Майерс-Бриггс
Ещё задолго до появления соционики подобные группы в американской типологии Майерс-Бриггс стали изучаться группы, основанные на общности 2-х (из 4-х) юнговских признаков. СначалаИзабел Майерс выделила и описала 4 группы установки на род деятельности (ST, SF, NT, NF). Затем, в сотрудничестве с другими исследователями (Линда Кирби и др.), она стала изучать и другие симметричные группы (например: FJ, FP, TJ, TP). Работа по их изучению и описанию была продолжена и после смерти И.Майерс.
В середине 1980-х гг. появились так называемые “темпераменты Кирси”. Профессор Дэйвид Кирси заявил, что известные темпераменты Гиппократа – Галена (холерики, сангвиники и т.д.) – не что иное, как группы типов Майерс-Бриггс: NT, NF, SP, SJ. К большому сожалению, несмотря на очевидные натяжки и логические ошибки в данной гипотезе, она получила большое распространение в США. Хотя, с другой стороны, в исследовательских публикациях американские типоведы предпочитают опираться на традиционные группы, по сходству 2-х из 4-х признаков.
Хотя американское типоведение использует функции и модель (см., напр., Л.Беренс), однако не использует малые группы по общей сильной функции (исключение – книга супругов Тайгеров Just Types, в русском переводе “Читать человека, как книгу”, где приведена попытка описать подобные группы). Наконец, поскольку в американском типоведении нет ни одной общепризнанной теории интертипных отношений, то не используются и группы, образованные по принципу симметрии отношений.
Малые группы в соционике
Кардинальным отличием соционики от американского типоведения является то, что типоведение интересовалось прежде всего личностными свойствами типов, тогда как соционика была ориентирована на отношения. “Ноу-хау” соционики – гипотеза о дуальности.
Раньше других малых групп в соционике были выделены и описаны квадры (группы из двух дуальных пар, которые отличаются друг от друга лишь порядком сильных функций). Эти группы кардинально отличаются от американских – в них не совпадает ни один из юнговских признаков. Тем не менее, квадра представляет собой достаточно устойчивую группу; нередко квадры образуются стихийно.
Существует два различных подхода в изучении малых групп.
Подход Рейнина – описание взаимодействия внутри группы
Г.Рейнин, а позднее – представители “вильнюсской школы” (Ф.Шехтер, Е.Шепетько и др.) описывали малые группы с точки зрения взаимодействия внутри этой группы. Что же касается характеристик той или иной конкретной малой группы (т.е., например, не “вообще букета”, а отдельно – “букета экстравертов-иррационалов”, “букета экстравертов-рационалов” и т.д.), то ни Рейнин, ни “вильнюсская школа” этим вопросом не занимались (что вообще-то немного удивительно, так как именно исследования в этом направлении могли бы прояснить вопрос о “признаках Рейнина”). Даже описания 4-х “клубов” появились в работах Рейнина довольно поздно, при этом почти полностью повторяют то, что ранее писала А.Аугустинавичюте.
Подход Гуленко – описание общих свойств группы
Иначе подошёл к этой проблеме В.Гуленко. В первой половине 1990-х гг. он составил описания практически всех возможных “малых групп” – как образованных по базису Юнга, так и по симметрии отношений. Хотя его описания, возможно, не всегда удачны, однако в этом направлении он один сделал едва ли не больше, чем все американские исследователи, работающие над проблемой “малых групп”. В частности, “клубы”, исследованные Гуленко, часто используются в соционических книгах и публикациях, посвящённых профессиональной ориентации и работе с кадрами. Позднее Н.Прилепская в книге “Ваш ребёнок: какой он?” опубликовала доработанные и усовершенствованные описания “малых групп”.
Малые группы можно образовывать тремя способами: 1) по двум совпадающим признакам из “базиса Юнга”; 2) по общей сильной функции; 3) по симметрии отношений в группе.
1. Группы по совпадению 2-х юнговских признаков
(подобные группы известны и у американских сторонников типологии Майерс-Бриггс)
| Название (Гуленко, Рейнин, Шепетько) | Какие признаки (функции) совпадают | Пример группы |
|---|---|---|
| “Клуб” (установка на род деятельности) | Интуиция/сенсорика и логика/этика | ИЛЭ, ИЛИ, ЛИЭ, ЛИИ |
| “Букет” (соционический темперамент) | Экстраверсия/интроверсия и рациональность/иррациональность | ИЛЭ, ИЭЭ, СЛЭ, СЭЭ |
| Стимульная группа | Экстраверсия/интроверсия и интуиция/сенсорика | ИЛЭ, ИЭЭ, ЛИЭ, ЭИЭ |
| Группа аргументации (“1-я группа здоровья”) | Логика/этика и рациональность/иррациональность | ИЛЭ, ИЛИ, СЛЭ, СЛИ |
| Группа коммуникабельности | Логика/этика и экстраверсия/интроверсия | ИЛЭ, СЛЭ, ЛИЭ, ЛСЭ |
| Группа установки восприятия (“2-я группа здоровья”) | Интуиция/сенсорика и рациональность/иррациональность | ИЛЭ, ИЭЭ, ИЛИ, ИЭИ |
2. Группы по совпадению функции в блоке ЭГО Модели А
(только в соционике)
| Название | Какие функции совпадают | Пример группы |
|---|---|---|
| Группа мировоззрения | Функция восприятия ( |
ИЛЭ, ИЭЭ, ЛИИ, ЭИИ |
| Группа образа действия | Функция суждения ( |
ИЛЭ, СЛЭ, ЛИИ, ЛСИ |
3. Группы, образованные по принципу симметрии отношений
(только в соционике)
| Название (Гуленко, Рейнин, Шепетько) | Принцип построения | Пример группы |
|---|---|---|
| Квадра | Две дуальных пары, объединённых зеркальными отношениями | ИЛЭ, СЭИ, ЛИИ, ЭСЭ |
| Квадрат | Две дуальных пары, объединённых “родственными” отношениями | ИЛЭ, СЭИ, ИЭЭ, СЛИ |
| Деловой квадрат | Две дуальных пары, объединённых “деловыми” отношениями | ИЛЭ, СЭИ, СЛЭ, ИЭИ |
| Группа двойной активации | Две квазитождественных пары активаторов | ИЛЭ, ЛИЭ, СЭЭ, ЭСЭ |
| Группа блокировки | Две дуальных пары, объединённых отношениями погашения | ИЛЭ, СЭИ, ИЛИ, СЭЭ |
| Лабиринт | Две конфликтных пары, объединённых зеркальными отношениями | ИЛЭ, ЛИИ, СЭЭ, ЭСИ |
| Группа мобилизации | Две квазитождественных дуальных пары | ИЛЭ, СЭИ, ЛИЭ, ЭСИ |
| Кольцо заказа | Кольцо из 4 типов, объединённых отношениями социального заказа | ИЛЭ, ЭИЭ, СЭЭ, ЛСЭ |
| Кольцо ревизии | Кольцо из 4 типов, объединённых отношениями социальной ревизии | ИЛЭ, ЛСИ, СЭЭ, ЭИИ |
Опираясь на те же принципы симметрии отношений, можно построить и более экзотические сочетания типов (некоторые из них упомянуты в книге В.Гуленко и В.Тыщенко “Юнг в школе”, а также в обзорной статье Е.Шепетько), однако вопрос о практической пользе таких сочетаний и об устойчивости таких групп остаётся открытым.
Сводная таблица малых групп
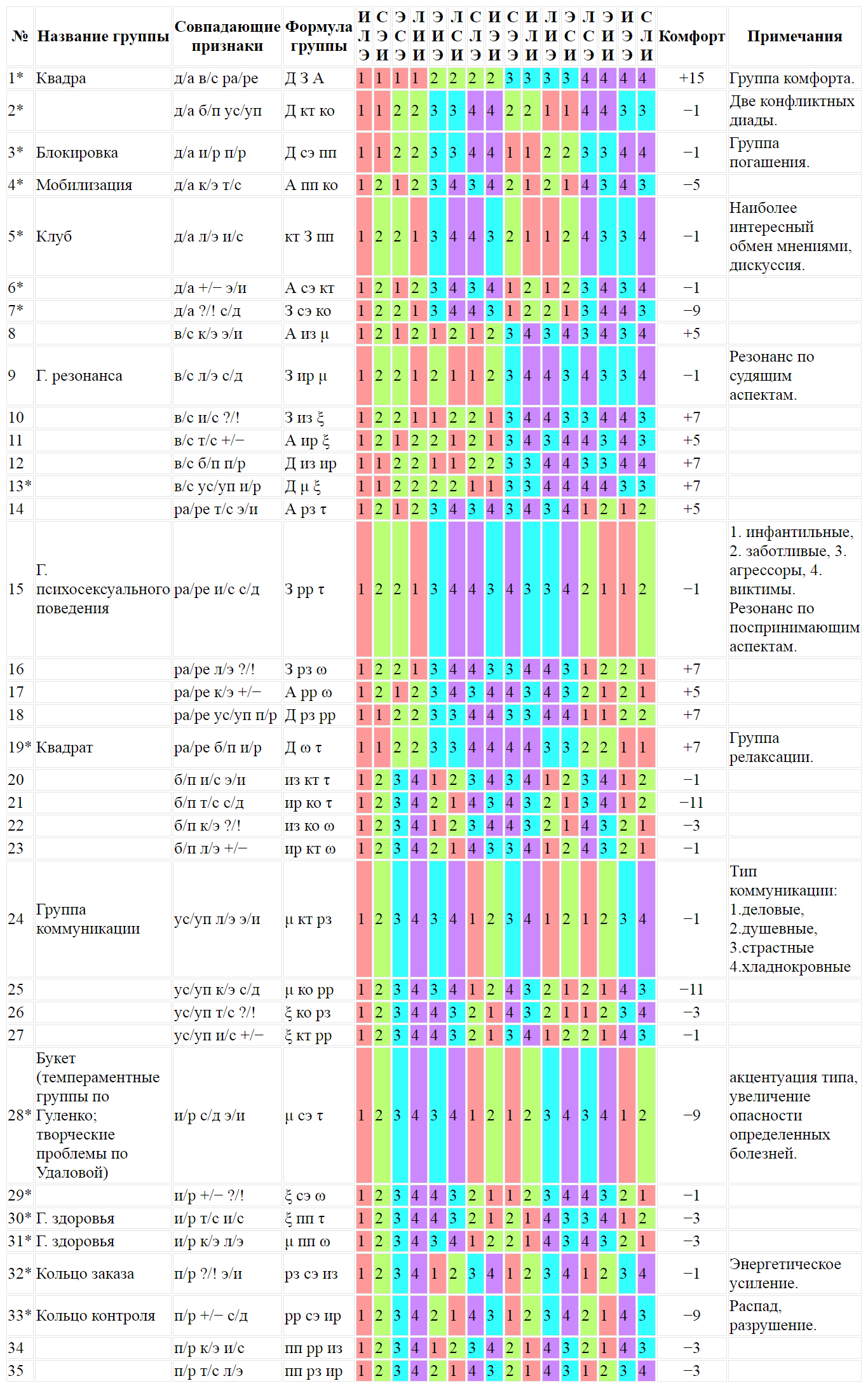
Условные обозначения отношений:Знаком * (звёздочка) обозначены симметричные группы.
- Д — дуальные;
- А — активации;
- З — зеркальные;
- сэ — супер-эго;
- пп — полного погашения;
- кт — квазитождества;
- ко — конфликтные;
- τ, ξ, μ, ω — типы отношений по Рейнину, которым не даны названия;
- из, рз — иррациональный и рациональный заказ соответственно;
- ир, рр — иррациональная и рациональная ревизия соответственно.
Условные обозначения признаков Рейнина:
- э/и — экстраверсия — интроверсия;
- с/д — статика — динамика;
- ?/! — квестимность — деклатимность;
- +/− — позитивизм — негативизм;
- и/с — интуиция — сенсорика;
- л/э — логика — этика;
- т/с — тактика — стратегия;
- к/э — конструктивизм — эмотивизм;
- п/р — процесс — результат;
- и/р — иррациональность — рациональность;
- ус/уп — уступчивость — упрямство;
- б/п — беспечность — предусмотрительность;
- ра/ре — рассудительность — решительность;
- в/с — весёлость — серьёзность;
- а/д — аристократизм — демократизм.
Комфортность групп
Простой способ оценки комфортности — алгебраическая сумма оценок интертипных отношений в группе.
| Группы | Коэффициент комфортности |
|---|---|
| 1 | +15 |
| 10, 12, 13, 16, 18, 19 | +7 |
| 8, 11, 14, 17 | +5 |
| 2, 3, 5, 6, 9, 15, 20, 23, 24, 27, 29, 32 | −1 |
| 22, 26, 30, 31, 34, 35 | −3 |
| 4 | −5 |
| 7, 28, 33 | −9 |
| 21, 25 | −11 |
См. также:
- Миронов В.В. “Формирование коллективов с учетом коэффициента комфортности в малых социальных группах“
- Субботин С.А. “Стили планирования“
- Признаки Рейнина
- «Информационные аспекты» (аспекты информационного метаболизма)
- Модель А
- Интертипные отношения
(с) http://www.socioniko.net; http://www.wikiznanie.ru; http://ru.wikipedia.org
